目次
言葉の使い分け
熱の分野では、言葉の使いわけが重要です。
講座ビデオでも、この違いについては詳しく説明されています。
それぞれの用語に関して、知子の情報には以下のように記録しました。
言葉だけでは、その違いを理解することは難しいですね。
分かったような、分からないような曖昧な状態です。
しっかりと理解しておくために、例をいくつか考えながら定着させていきます。
熱の正体は?
物質をミクロの状態まで見ていくと、原子や分子の集まりであることは化学で学びました。
熱が生じるのは、この分子または原子間の運動の差が関係しています。
ではここで、ある気体の分子の状態を考えてみます。
高温と低温の温度差のある気体を接触させた場合、どうなるでしょうか?

高温の状態では、分子は激しく運動しています。
一方、低温の場合は、分子の動きが高温に比べて緩やかです。
高温、低温の異なる2つの気体(物質)が接触すると、相互の分子や原子が衝突を繰り返し、相互の分子がもつ動きが平均化して同じ動きになっていきます。
この状態が熱平衡と言い、温度は等温になります。
例えば、発熱したときに氷枕などをつかって、熱を下げますよね。
氷枕や氷水に浸したタオルなどは、こまめに変えないと冷たさがなくなってしまいます。
これは体内の熱がタオルに伝わり、等温になるからです。
熱は必ず高温から低温へ伝わります。
この伝わる熱(エネルギー)の量のことを熱量と言います。
単位はJ(ジュール)で表します。
温度とは
温度(英語: temperature)とは、温冷の度合いを表す指標のことです。
つまり、熱運動の激しさを表す尺度になります。
上の図で、高温の温度は100度、低温の温度は10度でした。
高温のほうが、熱運動が激しいので、数値が大きくなりますね。
温度の表し方には2種類あります。
セルシウス温度と摂氏温度があります。
セルシウス温度は、私たちがよく使っている温度です。
1気圧の状態で、水の氷点を0度、沸点を100度として、100等分したものを1度(℃)とします。
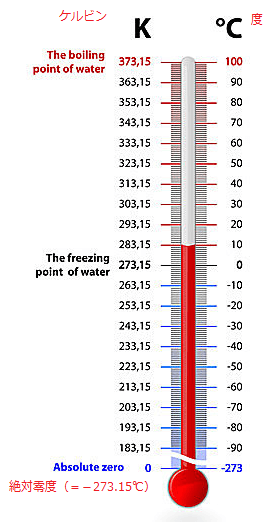
引用(日本気象協会)
K(ケルビン)で表す絶対温度は、分子や原子の運動が完全に停止する温度を絶対零度0ケルビン(K)(−273.15°C)と定義しています。
つまり、セルシウス温度0度は、絶対温度で表すと、273.15ケルビンになります。
比熱とは
比熱について考えてみます。
まず、鉄のフライパンと土鍋を同じ火力で温めたとします。
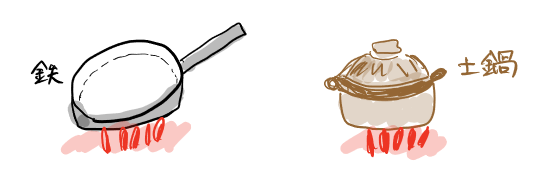
お料理をした方は感覚的にわかると思いますが、どちらが温まりやすいですか?
鉄のフライパンですよね?
目を離していると、あっという間に焦がしてしまったりします。
一方、土鍋はじっくりコトコトと加熱して温めるイメージがありませんか?
鉄のフライパンに比べて、温まる速度はゆっくりです。
この時、加熱する温度は同じです。
つまり与えられている熱量は同じになります。熱の伝わり方が異なるわけです。
では火を止めた後、鉄のフライパンは少し時間をおけば一気に冷えますが、土鍋はどうでしょうか?
温かさが鉄のフライパンより持続しますよね。
鉄のフライパンは、温まりやすく、冷めやすい。
土鍋は温まりにくく、冷めにくいと言えます。
これは物質によって比熱が異なるからです。
比熱は、1gあたりの物質の温度を1度上げるのに必要な熱量のことです。
比熱を比べると、鉄の比熱は0.461(J/g・K)、土鍋(陶器)の比熱は0.8(J/g・K)で、土鍋のほうが鉄の約2倍大きいことになります。
比熱が大きいということは、1度を上げるのに多くの熱が必要になります。
同じ重さの鉄と土鍋を比較すると、比熱が大きい土鍋は、温まるのに多くの熱が必要になります。つまり温まりにくいということです。
逆に比熱の小さい鉄は、温めるのに必要な熱が小さいので、温まりやすいのです。
同じ理由で、冷めやすさも説明できます。
比熱の大きい土鍋は多くの熱が必要になりますので、冷めにくくなります。鉄は熱が小さいので、冷めやすくなります。
熱容量とは
比熱の値に物体の質量を掛けたものを熱容量(単位は [J/K] )と呼びます。
その物体の温度を 1 K 上昇させるために必要な熱量を表しています。
同物質の場合、比熱は1gあたりの熱量ですが、熱容量は1gがm個ある場合の熱量です。
例えば1gを1K上昇させるのに必要な熱量が1J(ジュール)だとすると、熱容量はmg分の容量になるので、1K上昇させるのに必要な熱量は大きくなります。
鉄のフライパンが2つあり、容量が異なる場合を考えると分かりやすいと思います。
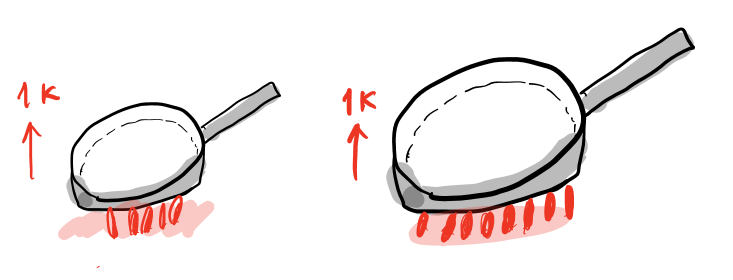
同じ1K温度を上げるために、当然容量の大きいフライパンのほうがより多くの熱量が必要になりますよね。
つまり、同じ熱量を与えた場合は、熱容量が大きければ大きいほど、温度の変化は小さくなるということです。
今日はここまで。
明日はこの知識にもう少し補足して、特許までむすびつけてみたいと思います。



















コメントを残す