目次
力学的エネルギー保存則
力学的エネルギー保存則に関する特許を取り上げてみます。
力学的エネルギーとは、運動エネルギーと位置エネルギーの和のことを表わします。
外部から摩擦などの力を受けない限り、力学的エネルギーは一定です。
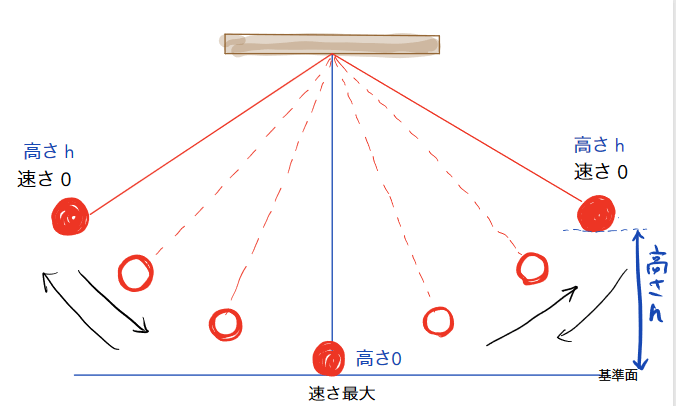
上の図のように、振り子の動きを追っていくと、運動エネルギーと位置エネルギーの関係性がよく分かります。
まず振り子を垂直に下した状態で、基準面を設定します。
基準面に振り子がある状態では、高さが0の状態です。
振り子を持ち上げて手を放すと、左右に弧を描いて動きます。
例えば、左側に振り子が移動した時に基準面から高さｈの状態で、振り子は一瞬止まり、再び重力の力によって、右側に揺れます。
高さが0の状態で、振り子自体の速度は最大になり、再び右へ揺れ、高さがｈの状態で、一瞬振り子が止まります。
この揺れを繰り返して、やがて振り子は止まります。
力学的エネルギーで考えると、
（左）速度が0なので、運動エネルギー（1/2mv²）は0になります。位置エネルギーは高さｈでは、mghです。
（垂直）高さが0なので、位置エネルギーは0になります。速度はこの時最大になるので、1/2mv²になります。
（右）速度が0なので、運動エネルギー（1/2mv²）は0になります。位置エネルギーは高さｈでは、mghです。
運動エネルギーが増えれば、位置エネルギーが減りますが、その総和（力学的エネルギー）は常に一定になります。
このことを力学的エネルギー保存則と言います。
垂直跳び測定装置と力学的エネルギー保存則
【公開番号】特開2019-20231(P2019-20231A)
【公開日】平成31年2月7日(2019.2.7)
【発明の名称】垂直跳び測定装置
【出願人】
【氏名又は名称】株式会社コンセプトアンドデザイン
この特許は、垂直跳び測定器に関するものです。
垂直跳び測定器といっても、いろいろなものがあります。
私が学生の頃に使ったものはこちら。
壁に目盛りがついたボードがあり、そのボードに垂直飛びをしながら片手でタッチするもの。
またはこのような測定器。腰にまきつけて、そのベルトの伸びを測定するもの。
またはこれ。
今回の特許で取り上げる垂直跳び測定器は、ベルトの着脱の手間や、マットスイッチの耐久性などの問題を解決したものです。
また人間以外の動物などの測定も可能で、かつ連続使用ができるなど、従来の測定器の問題点を解決するものとして、特許申請されています。
【背景技術】
【０００２】
従来の垂直跳び測定器は、被験者の腰にベルトで固定しておき、跳躍時に測定器に内蔵されている紐が伸びる構造を備え、跳躍前の紐の長さから跳躍後の紐の長さへの変位を計測し、測定結果として表示するものであった。
【０００３】
一方、計測を自動化した機器もある。例えば、ユーザに装着または把持されてユーザの動きに応じた加速度を検出する検出手段から加速度データを取得し、加速度データの解析を行って滞空時間を算出し、ジャンプ高さを算出する動作検出装置が知られている（特許文献１参照）。
【０００４】
また、被験者の離地から着地までの滞空時間をマットスイッチによって検出し、跳躍高さを検出する機能計測装置が知られている（特許文献２参照）。
ベルトを巻き付けたり、マットの耐久性の問題を解消するため、レーザー光を用いた測定装置です。
【００１０】
本発明は、垂直跳びの跳躍高さを測定する垂直跳び測定装置であって、 跳躍基準面から垂直方向に距離を置いて配置されてレーザ光を水平方向に放射する発光手段と、レーザ光を受光する受光手段と、この受光手段からの出力を用いて、測定対象に前記レーザ光が照射されている状態から照射されていない状態への移行を示す第１の出力変化、および測定対象にレーザ光が照射されていない状態から照射されている状態への移行を示す第２の出力変化を検出する処理を実行する出力変化検出手段と、この出力変化検出手段により第１の出力変化を検出した際の第１の時刻および第２の出力変化を検出した際の第２の時刻を取得する処理、または第１の出力変化の検出時から第２の出力変化の検出時までの時間間隔を計測する処理を実行する計時手段と、この計時手段により取得した第１の時刻と第２の時刻との差分から測定対象の滞空時間を算出するか、または計時手段により計測した時間間隔を測定対象の滞空時間とし、さらに、この滞空時間および重力加速度を用いて測定対象の跳躍高さを算出する処理を実行する跳躍高さ算出手段と、この跳躍高さ算出手段により算出した跳躍高さを出力する処理を実行する出力処理手段とを備えたことを特徴とするものである。
測定器はこちら。
発光ユニットから、受光ユニットにむかって、レーザー光が放射されます。
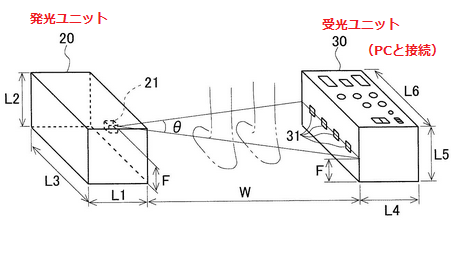
レーザー光には、可視光線レーザーおよび赤外線レーザーが用いられています。
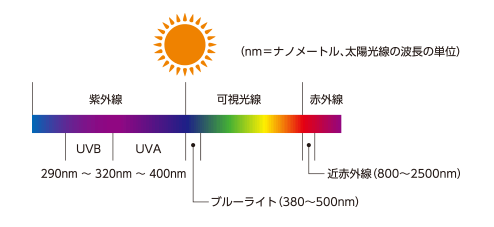引用：https://www.hikari-rouka.org/knowledge/sunlight/
【００２５】
このように発光手段と受光手段とが分離され、かつ、扇状に拡がるレーザ光を放射する構成とした場合には、跳び上がる際の測定対象の位置（測定対象が人間の場合には、通常は足の位置）と、跳躍基準面への落下（着地等）の際の測定対象の位置とがずれていても測定を行うことが可能となる。
特徴のひとつとして発光されるレーザー光は水平方向に扇状に拡がる状態です。
扇状にすることで、数か所のレーザー光を測定できるため、跳ぶ位置がずれても測定ができるようになっています。
測定についての具体的な流れは以下の通り。
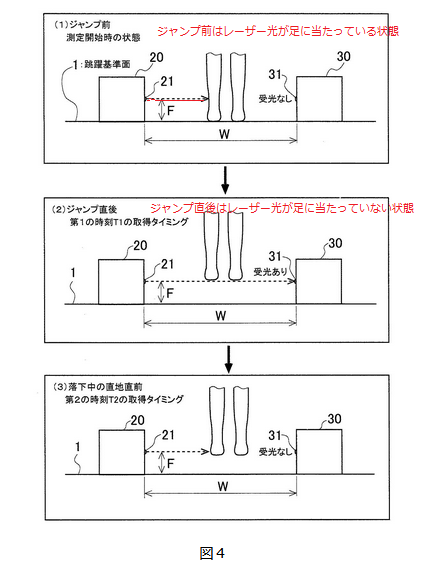
【００５７】
ここで、各受光手段３１からのアナログ出力のＡ／Ｄ変換後のデータについて、例えば、簡略化して（閾値を用いた受光の有無の判断結果として）、レーザ光を受光している状態を「１」とし、レーザ光を受光していない状態を「０」とすると、複数（４つ）の受光手段３１からの出力は、最初は、例えば（１，１，０，１）等となる。これは、図４の（１）ジャンプ前の状態のように、被験者の足がレーザ光を遮り、３番目の受光手段３１がレーザ光を受光していない状態である。
【００５８】
そして、（１，１，０，１）等の状態がしばらく続き（ここでは、途中で、例えば（１，０，１，１）や（１，０，０，１）等に変化したとしても、１つでも「０」が入っている限り、同じ状態が続いているものとみなす。）、その後に（１，１，１，１）という状態になったとすると、複数（４つ）の受光手段３１の全てが受光している状態に移行したことになる。これは、図４の（２）ジャンプ直後の状態のように、上昇する被験者の足がレーザ光の放射面の上側に達し、レーザ光を全く遮っていない状態である。従って、第１の出力変化を検出する処理は、複数（４つ）の受光手段３１のうちのいずれかがレーザ光を受光していない状態から、複数（４つ）の受光手段３１の全てがレーザ光を受光している状態への移行を示す出力変化を検出する処理であり、複数（４つ）の受光手段３１の全てがレーザ光を受光している状態であるか否かの判断を繰り返す処理となる。
跳ぶ前は、発光ユニットから放射されたレーザー光が足に当たった状態です。
足にあたっているレーザー光は、受光ユニットへのレーザー光が遮断された状態であり、この時に測定される数値は0（受光ユニットへ受光されていない）になります。
測定される数値の中に、ひとつでも0が含まれている場合は、地面に足が着いた状態（跳んでいない状態）ということになります。
図のように、ジャンプして受光ユニットで測定される数値がすべて1になっている場合、地面から足が離れた状態（跳んでいる状態）ということになります。連続して跳ぶ場合も、レーザー光の受光状態を数値から判断することができます。
【００６１】
ここで、（１，１，１，１）の状態がしばらく続いた後に、（１，０，１，１）という状態になったとすると、２番目の受光手段３１がレーザ光を受光していない状態に移行したことになる。これは、図４の（３）落下中の着地直前の状態のように、落下する被験者の足がレーザ光の放射面に達し、レーザ光を遮っている状態である。従って、第２の出力変化を検出する処理は、複数（４つ）の受光手段３１の全てがレーザ光を受光している状態から、複数（４つ）の受光手段３１のうちのいずれかがレーザ光を受光していない状態への移行を示す出力変化を検出する処理であり、複数（４つ）の受光手段３１のいずれかがレーザ光を受光していない状態であるか否かの判断を繰り返す処理となる。
力学的エネルギーの保存則の公式から、被験者の跳んだ高さを求めることができます。
（跳ぶ前）レーザー光が足に当たっている位置を基準として、A地点とします。
この時、A地点の高さは0とします。跳ぶ速度を初速度V０とします。
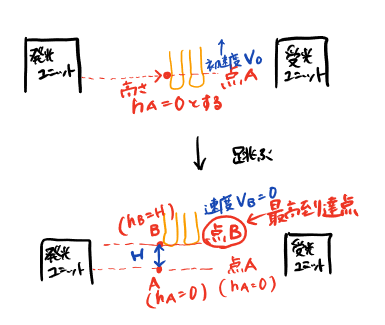
（跳んで最高到達点に達した時）
跳んだ後、A地点の基準点からｈBの高さに到達しました。このｈBの高さをHとします。
最高到達点に達しているので、速度は0になります。（VB＝0）
（１／２）ｍＶＡ²＋ｍｇｈＡ＝（１／２）ｍＶＢ²＋ｍｇｈＢ の力学的エネルギーの保存則の公式にあてはめると、
VA＝Vo、ｈA＝0なので左辺は （１／２）ｍＶ0²＋0…① となります。
右辺は、VB＝0、ｈB＝Hなので、0＋ｍｇH…② となります。
よって、①＝②を計算すると、両辺のmが消え、1/2を消すために両辺に2をかけます。
すると Vo²＝2ｇH となり、跳んだ距離Hを求めるためには、 H＝Vo²/２ｇ となります。
【００６５】
また、初速度（レーザ光の放射面の高さ位置を通過する際の速度）をＶ０とする。なお、本願明細書では、レーザ光の放射面の高さ位置を上昇時に通過する際の速度の大きさ、および落下時に通過する際の速度の大きさの双方をともに初速度と呼ぶ。自由落下では、最高到達点の速度の大きさはゼロであり、そこからレーザ光の放射面の高さ位置まで落下すると、滞空時間の半分の時間（ΔＴ／２）だけ重力加速度ｇが作用し続け、初速度Ｖ０に至ることになる。従って、重力加速度ｇをｔ＝０からｔ＝（ΔＴ／２）まで時間で積分した値がＶ０になるので、（ΔＴ／２）×ｇ＝Ｖ０が成立する。
【００６６】
一方、レーザ光の放射面の高さ位置（点Ａ）と、最高到達点（点Ｂ）との２点間で、力学的エネルギーの保存則を考えると、次の式が成立する。
【００６７】
（１／２）ｍＶＡ２＋ｍｇｈＡ＝（１／２）ｍＶＢ２＋ｍｇｈＢ
【００６８】
ここで、上記の式に、ＶＡ＝Ｖ０、ｈＡ＝０、ＶＢ＝０、ｈＢ＝Ｈを代入すると、次の式が成立するので、さらに、（ΔＴ／２）×ｇ＝Ｖ０を代入してＶ０を消すと、レーザ光の放射面の高さ位置（点Ａ）から最高到達点（点Ｂ）までの距離Ｈが求まる。
【００６９】
Ｖ０２／（２ｇ）＝Ｈ
【００７０】
そして、求めたＨに、オフセットＦを加えると、被験者の跳躍高さ（Ｈ＋Ｆ）を算出することができる。
まとめ
物理の公式や法則がどのように特許で使われているか、明細書の文字だけを追っているだけでは、理解ができないことが分かりました。
公式や法則を理解した上で、明細書の文字を図解化することで、明細書の言わんとすることが少し見えてくるような気がします。
この作業は時間もかかりますが、物理の知識だけを暗記する頭でっかちにならないように、地道な作業（物理から明細書）を続けていきます。
数か月後、もっと違った見方ができているように、自分の成長をはかる目安として、間違いも含めて、記録として残しておきます。
コメントを残す