目次
物理の勉強
現在、物理で仕事、エネルギーなどの分野に進んでいます。
これらの言葉は、日常でもよく使っている言葉です。
ですが、知っている意味をそのまま当てはめてしまうと、物理の分野では言葉のニュアンスが少し異なることに気付きます。
では、物理での仕事とは?エネルギーとは?
特許に結びつけながら考えてみます。
仕事=WORK?
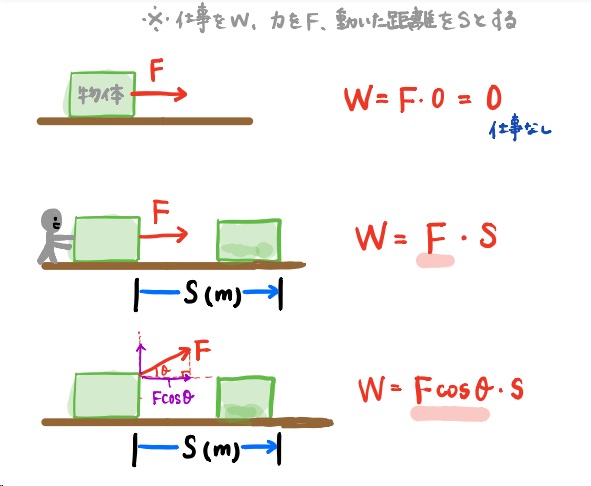
物理では、ある物体に一定の力(F)を加えた時に、静止したままの状態だと、仕事は0の状態です。
次に、物体に一定の力をかけ続け、力の向きに物体がS(m)だけ動かしたとします。
この時、力が物体に仕事をしたことになります。
物体になされた仕事は、物体にかけた力 と 物体が移動した距離 の 積 で表すことができます。
よって、W=F・Sとなります。(上の図の真ん中)
図の真ん中と一番下のイラストは、力の傾きが違っています。
真ん中の場合、力は移動する方向と一致しています。一方、一番下のイラストでは、力には傾きがあり、角度θの方向です。
力の向きに角度があっても、同じようにS(m)物体は移動しています。
この場合、斜めに働く力Fは、物体が移動する方向の力(Fcosθ)と物体に対して垂直に働く力(Fsinθ)に分解できますが、今回は、物体が移動する方向の力のみを考えればよいので、W=Fcosθ・Sとなります。
仕事とエネルギーの関係
物体が仕事をする能力を持っているとき、その物体はエネルギーがあるという言い方をします。

英英辞典 Merriam Webster’s collegiate Dictionaryでenergy の意味を引くと
the capacity for doing work 書かれています。
資源エネルギー庁のサイトに書かれていたエネルギーの代表的な種類です。
・力学的エネルギー(運動エネルギー、位置エネルギー)
・化学エネルギー
・光エネルギー
・核エネルギー
・電気エネルギー
エネルギーの特徴として、エネルギーは変換して、熱や光、電気などいろいろなものに姿を変えることができます。
また、エネルギーは姿を変える前と後では、その総和は変わりません。
日常の言葉では「エネルギー切れ」と言ったりしますが、物理においては、Aというエネルギーを使って、Bというエネルギーに変換したことになります。つまり、Aというエネルギーを使いきってなくなったわけではなく、Aというエネルギーは0になり、その減った分のエネルギーがBというエネルギーに変わったと考えることになります。
具体的に力学的エネルギーを例に考えてみます。
位置エネルギーと運動エネルギー
力学的エネルギーを考える時に、振り子がよく例として使われます。
運動エネルギー(kinetic energy)とは
物体の運動に伴うエネルギー。物体の速度を変化させる際に必要な仕事。
引用:Wikipediaより
位置エネルギー(potential energy)とは
物体が「ある位置」にあることで物体にたくわえられるエネルギーのこと。
ポテンシャルエネルギーとも言う。
引用:Wikipediaより、
この運動エネルギーと位置エネルギーが変換する例として、振り子がよくつかわれます。

垂直に静止している振り子を斜め上に引っ張り、Aの地点で手を離す直前は、物体がエネルギーを蓄えている位置エネルギーが最大の状態です。
この時の位置エネルギーを10とします。
次に手を離し、振り子は重力により下に引かれると加速し、運動エネルギーになり、一番下(Bの地点)で最高速になります。
この時、位置エネルギーは0の状態、逆に運動エネルギーは最大の10の状態になります。 エネルギーの変換が起こっている
その後、振り子はA’の地点まで弧を描きながら揺れ、A’の地点で再び位置エネルギーを蓄えて、運動エネルギーへの変換する揺れを繰り返します。
このように、
(運動エネルギー) + (位置エネルギー) = 一定
の状態のことを、力学的エネルギー保存の法則が成り立つと言います。
特許について
力学的エネルギーを技術に活用した特許を検索してみました。
機械や自動車等に使われている特許もありましたが、「水の浄化」×力学的エネルギーというキーワードで特許があったので、今回はこちらを取り上げてみます。
人類にとって貴重な資源の水。
飲み水や工業・農業でも幅広く利用されており、水の浄化はあらゆる技術が活用されています。
薬剤注入による化学を活かした方法やろ過や蒸発などの反応を利用した方法などがありますが、下記の特許では力学的エネルギーの考えが反映されていました。
【公開番号】特開2012-17557(P2012-17557A)
【公開日】平成24年1月26日(2012.1.26)
【発明の名称】河川水を用いた無動力海水または湖沼浄化システム
【発明の詳細な説明】
【技術分野】
【0001】
河川水あるいは湖沼水または雨水が保有する力学的エネルギーを利用して、海水あるいは湖沼の循環および浄化を行う技術に関する。
【0020】
図1を用いて、本発明の原理および概念を説明する。図は河道に沿う鉛直断面図である。説明の簡便のため、直線の導水管を考え、河口の地形は鉛直断面とする。
河川水を分流する上流の地点をAとし、その標高をH、地点Aにおける河川水の流速をVa、圧力をPaとする。A点において河川水の一部を分流させ、導水管によって河口の海中(地点C)に導き、そこで海水に注入する。注入地点Cの水深をHc、流速をVc、圧力をPc、地点Cの直上の海面気圧をPbとする。ここで全体の流れの場が時間とともに変化しない定常状態を仮定し、また、河川水と導水管の摩擦は無いと仮定する。このような系では、分流地点Aから注入地点Cに到る水塊の流速、圧力、位置エネルギーおよび運動エネルギーの関係は、力学的エネルギー保存の法則(この場合はベルヌーイの定理)によって支配される。河川水の密度を1kg/1m³、重力加速度をg、位置エネルギーの基準面を海面とすると、この定理は以下のように記述される。
Vc² – 2gHc+ 2Pc =Va²+2gH+2Pa (1)
Pc=Pb+gHc (2)
(1)、(2)より、
Vc2 =Va2+2gH+2(Pb- Pa) (3)
 力学的エネルギーをもつ河川水を、海水や湖水に注入して、密度差を利用して海水や湖水を浄化するというものです。
力学的エネルギーをもつ河川水を、海水や湖水に注入して、密度差を利用して海水や湖水を浄化するというものです。
海水の密度を調べると、1.02 ~ 1.035 g/cm³。
この特許では、河川水の密度は1kg/1m³と記載されています。
河川水は海水に比べて密度が小さいことになります。(密度差がある)
水のような液体について力学的エネルギーを考える際には、位置と運動のエネルギーの他に、圧力のエネルギーも考える必要があります。
(ベルヌーイの定理と言います)

上の図は、配管に流体が流れている様子を表しています。
ベルヌーイの定理では、同一の流線上の2点間(点Aと点B)において、運動エネルギー・位置エネルギー・圧力エネルギーの和が一定になります。
流体の場合のエネルギー保存則が、ベルヌーイの定理です。
関係式(3)は、注入地点における河川水の流速は、分流地点の標高と流速、分流地点と注入地点の地上気圧差のみで決まり、注入される地点の水深および導水管の傾斜および形状には依存しないことを示している。また、分流地点の流速が速いほど、標高が高いほど、両地点の地上気圧差が大きいほど、注入地点の流速は大きくなることを意味している。水力学の原理は、ひとたびこのような導水管を設置すれば、河川水は、この関係式を満足するように、無動力で永久に自動的に海中に注入される。
力学的エネルギーをもった流体のような河川水は、導水管を作ってしまえば、あとは海中へ自動的に注入され、海水と河川水の密度差によって、河川水が上昇し、海水が下降する対流が自動的に起こり、海水が循環される仕組みです。
自然のエネルギーを動力にして、密度差による循環力を活用した浄化方法でした。
まとめ
今回の特許は理解度は70%くらいです。
自分が学んだ内容からなんとか特許明細書の言わんとすることを紐解き、「すでに知っている知識」と「知らない知識」を浮かび上がらせ、その足りない知識を調査して読み込むことで、特許の全体像が少しは見えてくるようになるということが実感できた内容の特許でした。
特許の中で、公式がさらっと使われていることもあり、その公式の意味を数分間で理解するためには、物理の勉強が暗記だけでは通用しないことも再確認しました。
ベルヌーイの定理は、特許でも多くの分野で概念が使われているので、別な切り口でもう少し知識の補充が必要です。


















コメントを残す